An R package for space-time anomaly detection using scan statistics.
To install the latest (CRAN) release of this package, type the following:
install.packages("scanstatistics")To install the development version of this package, type this instead:
devtools::install_github("promerpr/scanstatistics")Scan statistics are used to detect anomalous clusters in spatial or space-time data. The gist of the methodology, at least in this package, is this:
scan_eb_poisson: computes the
expectation-based Poisson scan statistic (Neill 2005).scan_pb_poisson: computes the
(population-based) space-time scan statistic (Kulldorff 2001).scan_eb_negbin: computes the
expectation-based negative binomial scan statistic (Tango et
al. 2011).scan_eb_zip: computes the
expectation-based zero-inflated Poisson scan statistic (Allévius &
Höhle 2017).scan_permutation: computes the
space-time permutation scan statistic (Kulldorff et al. 2005).scan_bayes_negbin: computes the
Bayesian Spatial scan statistic (Neill 2006), extended to a space-time
setting.knn_zones: Creates a set of spatial
zones (groups of locations) to scan for anomalies. Input is a
matrix in which rows are the enumerated locations, and columns the k
nearest neighbors. To create such a matrix, the following two functions
are useful:
coords_to_knn: use
stats::dist to get the k nearest neighbors of each location
into a format usable by knn_zones.dist_to_knn: use an already computed
distance matrix to get the k nearest neighbors of each location into a
format usable by knn_zones.flexible_zones: An alternative to
knn_zones that uses the adjacency structure of locations to
create a richer set of zones. The additional input is an adjacency
matrix, but otherwise works as knn_zones.score_locations: Score each location
by how likely it is to have an ongoing anomaly in it. This score is
heuristically motivated.top_clusters: Get the top k space-time
clusters, either overlapping or non-overlapping in the spatial
dimension.df_to_matrix: Convert a data frame
with data for each location and time point to a matrix with locations
along the column dimension and time along the row dimension, with the
selected data as values.To demonstrate the scan statistics in this package, we will use a dataset of the annual number of brain cancer cases in the counties of New Mexico, for the years 1973-1991. This data was studied by Kulldorff (1998), who detected a cluster of cancer cases in the counties Los Alamos and Santa Fe during the years 1986-1989, though the excess of brain cancer in this cluster was not deemed statistically significant. The data originally comes from the package rsatscan, which provides an interface to the program SaTScan, but it has been aggregated and extended for the scanstatistics package.
To get familiar with the counties of New Mexico, we begin by plotting
them on a map using the data frames NM_map and
NM_geo supplied by the scanstatistics package:
library(scanstatistics)
library(ggplot2)
# Load map data
data(NM_map)
data(NM_geo)
# Plot map with labels at centroids
ggplot() +
geom_polygon(data = NM_map,
mapping = aes(x = long, y = lat, group = group),
color = "grey", fill = "white") +
geom_text(data = NM_geo,
mapping = aes(x = center_long, y = center_lat, label = county)) +
ggtitle("Counties of New Mexico")
We can further obtain the yearly number of cases and the population
for each country for the years 1973-1991 from the data table
NM_popcas provided by the package:
data(NM_popcas)
head(NM_popcas)
#> year county population count
#> 1 1973 bernalillo 353813 16
#> 2 1974 bernalillo 357520 16
#> 3 1975 bernalillo 368166 16
#> 4 1976 bernalillo 378483 16
#> 5 1977 bernalillo 388471 15
#> 6 1978 bernalillo 398130 18It should be noted that Cibola county was split from Valencia county in 1981, and cases in Cibola have been counted to Valencia in the data.
The Poisson distribution is a natural first option when dealing with
count data. The scanstatistics package provides the two
functions scan_eb_poisson and scan_pb_poisson
with this distributional assumption. The first is an expectation-based1 scan statistic for univariate
Poisson-distributed data proposed by Neill et al. (2005), and we focus
on this one in the example below. The second scan statistic is the
population-based scan statistic proposed by Kulldorff (2001).
The first argument to any of the scan statistics in this package
should be a matrix (or array) of observed counts, whether they be
integer counts or real-valued “counts”. In such a matrix, the columns
should represent locations and the rows the time intervals, ordered
chronologically from the earliest interval in the first row to the most
recent in the last. In this example we would like to detect a potential
cluster of brain cancer in the counties of New Mexico during the years
1986-1989, so we begin by retrieving the count and population data from
that period and reshaping them to a matrix using the helper function
df_to_matrix:
library(dplyr)
#>
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#>
#> filter, lag
#> The following objects are masked from 'package:base':
#>
#> intersect, setdiff, setequal, union
counts <- NM_popcas %>%
filter(year >= 1986 & year < 1990) %>%
df_to_matrix(time_col = "year", location_col = "county", value_col = "count")
#> Warning: `spread_()` was deprecated in tidyr 1.2.0.
#> Please use `spread()` instead.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was generated.The second argument to scan_eb_poisson should be a list
of integer vectors, each such vector being a zone, which is the
name for the spatial component of a potential outbreak cluster. Such a
zone consists of one or more locations grouped together according to
their similarity across features, and each location is numbered as the
corresponding column index of the counts matrix above
(indexing starts at 1).
In this example, the locations are the counties of New Mexico and the
features are the coordinates of the county seats. These are made
available in the data table NM_geo. Similarity will be
measured using the geographical distance between the seats of the
counties, taking into account the curvature of the earth. A distance
matrix is calculated using the spDists function from the
sp package, which is then passed to dist_to_knn
and on to knn_zones:
library(sp)
library(magrittr)
# Remove Cibola since cases have been counted towards Valencia. Ideally, this
# should be accounted for when creating the zones.
zones <- NM_geo %>%
filter(county != "cibola") %>%
select(seat_long, seat_lat) %>%
as.matrix %>%
spDists(x = ., y = ., longlat = TRUE) %>%
dist_to_knn(k = 15) %>%
knn_zonesThe advantage of expectation-based scan statistics is that parameters
such as the expected value can be modelled and estimated from past data
e.g. by some form of regression. For the expectation-based Poisson scan
statistic, we can use a (very simple) Poisson GLM to estimate the
expected value of the count in each county and year, accounting for the
different populations in each region. Similar to the counts
argument, the expected values should be passed as a matrix to the
scan_eb_poisson function:
mod <- glm(count ~ offset(log(population)) + 1 + I(year - 1985),
family = poisson(link = "log"),
data = NM_popcas %>% filter(year < 1986))
ebp_baselines <- NM_popcas %>%
filter(year >= 1986 & year < 1990) %>%
mutate(mu = predict(mod, newdata = ., type = "response")) %>%
df_to_matrix(value_col = "mu")Note that the population numbers are (perhaps poorly) interpolated from the censuses conducted in 1973, 1982, and 1991.
We can now calculate the Poisson scan statistic. To give us more
confidence in our detection results, we will perform 999 Monte Carlo
replications, by which data is generated using the parameters from the
null hypothesis and a new scan statistic calculated. This is then
summarized in a P-value, calculated as the proportion of times the
replicated scan statistics exceeded the observed one. The output of
scan_poisson is an object of class “scanstatistic”, which
comes with the print method seen below.
set.seed(1)
poisson_result <- scan_eb_poisson(counts = counts,
zones = zones,
baselines = ebp_baselines,
n_mcsim = 999)
print(poisson_result)
#> Data distribution: Poisson
#> Type of scan statistic: expectation-based
#> Setting: univariate
#> Number of locations considered: 32
#> Maximum duration considered: 4
#> Number of spatial zones: 415
#> Number of Monte Carlo replicates: 999
#> Monte Carlo P-value: 0.005
#> Gumbel P-value: NULL
#> Most likely event duration: 4
#> ID of locations in MLC: 15, 26As we can see, the most likely cluster for an anomaly stretches from 1986-1989 and involves the locations numbered 15 and 26, which correspond to the counties
counties <- as.character(NM_geo$county)
counties[c(15, 26)]
[1] "losalamos" "santafe" These are the same counties detected by Kulldorff (1998), though their analysis was retrospective rather than prospective as ours was. Ours was also data dredging as we used the same study period with hopes of detecting the same cluster.
We can score each county according to how likely it is to be part of
a cluster in a heuristic fashion using the function
score_locations, and visualize the results on a heatmap as
follows:
# Calculate scores and add column with county names
county_scores <- score_locations(poisson_result, zones)
county_scores %<>% mutate(county = factor(counties[-length(counties)],
levels = levels(NM_geo$county)))
# Create a table for plotting
score_map_df <- merge(NM_map, county_scores, by = "county", all.x = TRUE) %>%
arrange(group, order)
# As noted before, Cibola county counts have been attributed to Valencia county
score_map_df[score_map_df$subregion == "cibola", ] %<>%
mutate(relative_score = score_map_df %>%
filter(subregion == "valencia") %>%
select(relative_score) %>%
.[[1]] %>% .[1])
ggplot() +
geom_polygon(data = score_map_df,
mapping = aes(x = long, y = lat, group = group,
fill = relative_score),
color = "grey") +
scale_fill_gradient(low = "#e5f5f9", high = "darkgreen",
guide = guide_colorbar(title = "Relative\nScore")) +
geom_text(data = NM_geo,
mapping = aes(x = center_long, y = center_lat, label = county),
alpha = 0.5) +
ggtitle("County scores")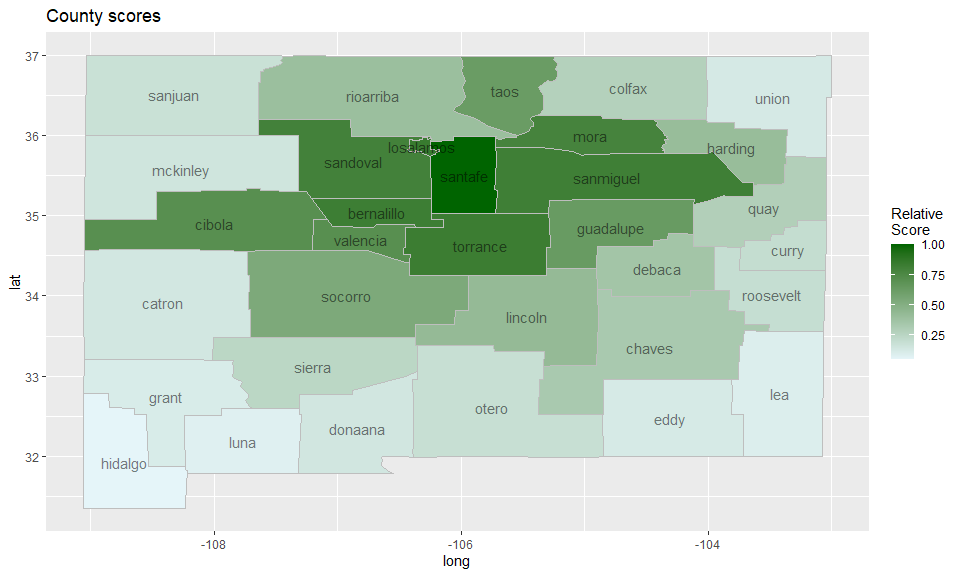
A warning though: the score_locations function can be
quite slow for large data sets. This might change in future versions of
the package.
Finally, if we want to know not just the most likely cluster, but say
the five top-scoring space-time clusters, we can use the function
top_clusters. The clusters returned can either be
overlapping or non-overlapping in the spatial dimension, according to
our liking.
top5 <- top_clusters(poisson_result, zones, k = 5, overlapping = FALSE)
# Find the counties corresponding to the spatial zones of the 5 clusters.
top5_counties <- top5$zone %>%
purrr::map(get_zone, zones = zones) %>%
purrr::map(function(x) counties[x])
# Add the counties corresponding to the zones as a column
top5 %<>% mutate(counties = top5_counties)The top_clusters function includes Monte Carlo and
Gumbel P-values for each cluster. These P-values are conservative, since
secondary clusters from the original data are compared to the most
likely clusters from the replicate data sets.
Other univariate scan statistics can be calculated practically in the same way as above, though the distribution parameters need to be adapted for each scan statistic.
If you think this package lacks some functionality, or that something needs better documentation, please open an issue here.
Allévius, B., M. Höhle (2017): An expectation-based space-time scan statistic for ZIP-distributed data, (under review).
Kleinman, K. (2015): Rsatscan: Tools, Classes, and Methods for Interfacing with SaTScan Stand-Alone Software, https://CRAN.R-project.org/package=rsatscan.
Kulldorff, M., Athas, W. F., Feuer, E. J., Miller, B. A., Key, C. R. (1998): Evaluating Cluster Alarms: A Space-Time Scan Statistic and Brain Cancer in Los Alamos, American Journal of Public Health 88 (9), 1377–80.
Kulldorff, M. (2001), Prospective time periodic geographical disease surveillance using a scan statistic, Journal of the Royal Statistical Society, Series A (Statistics in Society), 164, 61–72.
Kulldorff, M., Heffernan, R., Hartman, J., Assunção, R. M., Mostashari, F. (2005): A space-time permutation scan statistic for disease outbreak detection, PLoS Medicine, 2 (3), 0216-0224.
Neill, D. B., Moore, A. W., Sabhnani, M., Daniel, K. (2005): Detection of Emerging Space-Time Clusters, In Proceedings of the Eleventh ACM SIGKDD International Conference on Knowledge Discovery in Data Mining, 218–27. ACM.
Neill, D. B., Moore, A. W., Cooper, G. F. (2006): A Bayesian Spatial Scan Statistic, Advances in Neural Information Processing Systems 18: Proceedings of the 2005 Conference.
Tango, T., Takahashi, K. Kohriyama, K. (2011), A Space-Time Scan Statistic for Detecting Emerging Outbreaks, Biometrics 67 (1), 106–15.
Expectation-based scan statistics use past non-anomalous data to estimate distribution parameters, and then compares observed cluster counts from the time period of interest to these estimates. In contrast, population-based scan statistics compare counts in a cluster to those outside, only using data from the period of interest, and does so conditional on the observed total count.↩︎