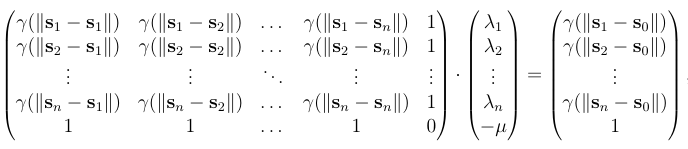
In this paper, we have observsed n curves χs1(t), …, χsn(t) in a region, where si = (θi, ηi), i = 1, …, n, and θi is the latitude and ηi is the longitude where the curve χsi was sampled. The goal of this package is to estimate an unsampled curve χs0(t) at s0 ∉ {s1, …, sn}. The Ideia proposed by Giraldo (2011) was simple: the curve χs0(t) is a linear combination of all curves χs1(t), …, χsn(t), i.e., \(\\widehat{\\chi\_{\\mathbf{s}\_0}}(t) = \\lambda\_1 \\chi\_{\\mathbf{s}\_1}(t) + \\lambda\_2 \\chi\_{\\mathbf{s}\_2}(t) + \\dots + \\lambda\_n \\chi\_{\\mathbf{s}\_1}(t)\) where λ1, …, λn is solution of the linear system given by
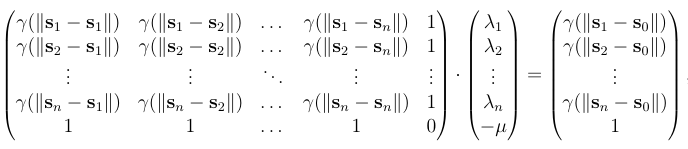
where μ is an constant from the method of Lagrange’s multipliers and the function γ(h) = ∫γ(h; t)*dt* is called the trace-variogram, where, for each t, γ(h; t) is the semivariogram for the process χs1(t), …, χsn(t). More precisely, for each t, a weakly and isotropic spatial process is assumed for χs1(t), …, χs**n(t) and the integration of the semivariogram is carried out. Usually, the integration in the equation (1) is approximated using a modified version of the empirical semivariogram. In this pcackage, we have used the Legendre-Gauss quadrature, which is simple and it explicitly used the definition of the semivariogram.
This package can be installed using the devtools
package.
devtools::install_github("gilberto-sassi/geoFourierFDA")In this package, we have used the temperature dataset present in the
package fda and
in the package geofd.
This dataset has temperature measurements from 35 weather stations from
Canada. This data can be downloaded at weather.gov.ca. For illustration, we
have separated the time series at The Pas station and used all
others stations to estimate the curve temperature at The
Pas.
# interpolating curve at Halifax using all remaining curves in the functional dataset
data(canada)
# Estimating the temperature at The Pas
geo_fda(canada$m_data, canada$m_coord, canada$ThePas_coord)# Coefficients of smoothing using Fourier series polynomial
# Coefficients of smoothing at The Pas
data(canada)
coefs <- coef_fourier(canada$ThePas_ts)# Coefficients of smoothing using Fourier series polynomial
# Coefficients of smoothing at The Pas
data(canada)
# coefficients of Fourier series polynomial
coefs <- coef_fourier(canada$ThePas_ts, m)
# points to evaluate curve at interval [-pi, pi]
x <- seq(from = -pi, to = pi, by = 0.01)
# smoothed curve at some points x
y_est <- fourier_b(coefs, x)Giraldo, R, P Delicado, and J Mateu. 2011. “Ordinary Kriging for Function-Valued Spatial Data.” Environmental and Ecological Statistics 18 (3): 411–26.