The conditional dependence structure (CDS) of a data matrix with \(p\) variables can be modeled as an undirected graph with \(p\) vertices, where two variables are connected if, and only if, the two variables are dependent given the remaining variables in the data. Gaussian graphical modeling (GGM) seeks to capture the CDS of the data under the assumption that the data are normally distributed. This distributional assumption is convenient for inference, as the CDS is given by the sparsity structure of the precision matrix, where the precision matrix is defined as the inverse covariance matrix of the data.
There is extensive GGM literature and many R packages for GGM,
however, all make the restrictive assumption that the precision matrix
is homogeneous throughout the data, or that there exists a partition of
homogeneous subgroups. covdepGE avoids this strong
assumption by utilizing information sharing to model the CDS as varying
continuously with an extraneous covariate. Intuitively, this implies
that observations having similar extraneous covariate values will have
similar precision matrices.
To facilitate information sharing while managing complexity,
covdepGE uses an efficient variational approximation
conducted under the novel weighted pseudo-likelihood framework proposed
by (1). covdepGE further accelerates inference by employing
parallelism and executing expensive iterative computations in C++.
Additionally, covdepGE offers a principled, data-driven
approach for hyperparameter specification that only requires the user to
input data and extraneous covariates to perform inference. Finally,
covdepGE offers several wrappers around
ggplot2 for seamless visualization of resulting estimates,
such as matViz, inclusionCurve, and the S3
method plot.covdepGE.
You can install the released version of covdepGE from CRAN with:
install.packages("covdepGE")And the development version from GitHub with:
# install.packages("devtools")
devtools::install_github("JacobHelwig/covdepGE")If you have an idea to improve covdepGE, considering forking the repo
and creating a pull request or opening an
issue.
library(covdepGE)
library(ggplot2)
# get the data
set.seed(12)
data <- generateData()
X <- data$X
Z <- data$Z
interval <- data$interval
prec <- data$true_precision
# get overall and within interval sample sizes
p <- ncol(X)
n <- nrow(X)
n1 <- sum(interval == 1)
n2 <- sum(interval == 2)
n3 <- sum(interval == 3)
# visualize the distribution of the extraneous covariate
ggplot(data.frame(Z = Z, interval = as.factor(interval))) +
geom_histogram(aes(Z, fill = interval), color = "black", bins = n %/% 5)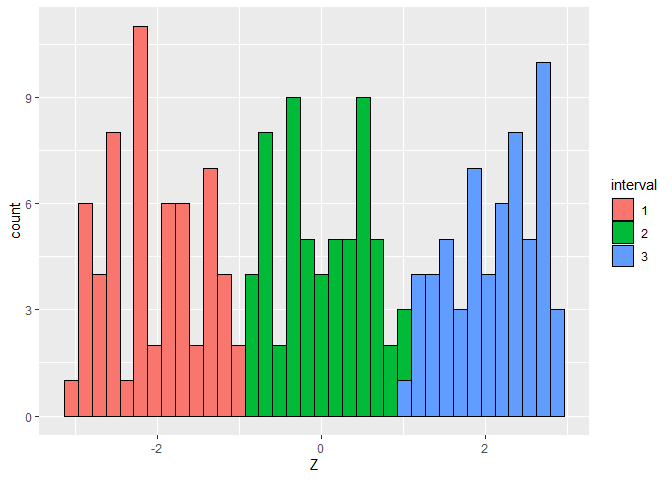
# visualize the true precision matrices in each of the intervals
# interval 1
matViz(prec[[1]], incl_val = TRUE) +
ggtitle(paste0("True precision matrix, interval 1, observations 1,...,", n1))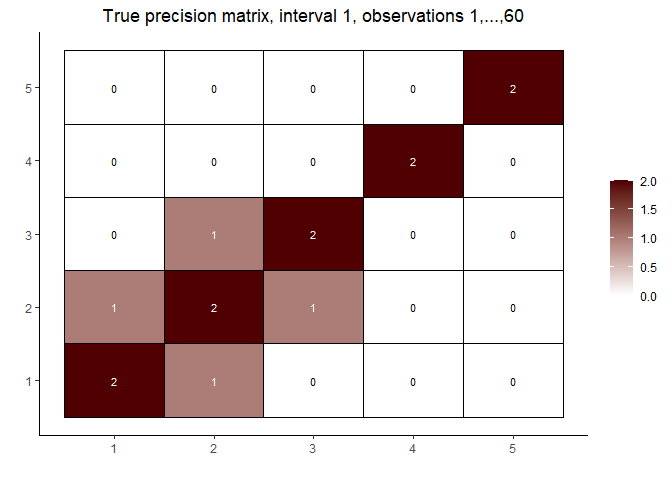
# interval 2 (varies continuously with Z)
cat("\nInterval 2, observations ", n1 + 1, ",...,", n1 + n2, sep = "")
#>
#> Interval 2, observations 61,...,120
int2_mats <- prec[interval == 2]
int2_inds <- c(5, n2 %/% 2, n2 - 5)
lapply(int2_inds, function(j) matViz(int2_mats[[j]], incl_val = TRUE) +
ggtitle(paste("True precision matrix, interval 2, observation", j + n1)))
#> [[1]]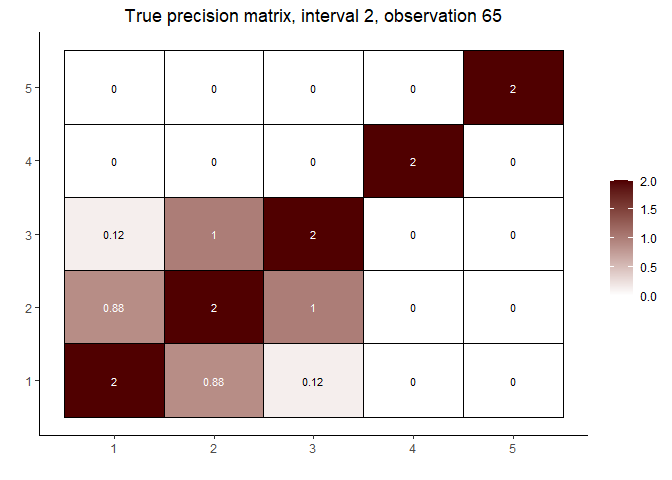
#>
#> [[2]]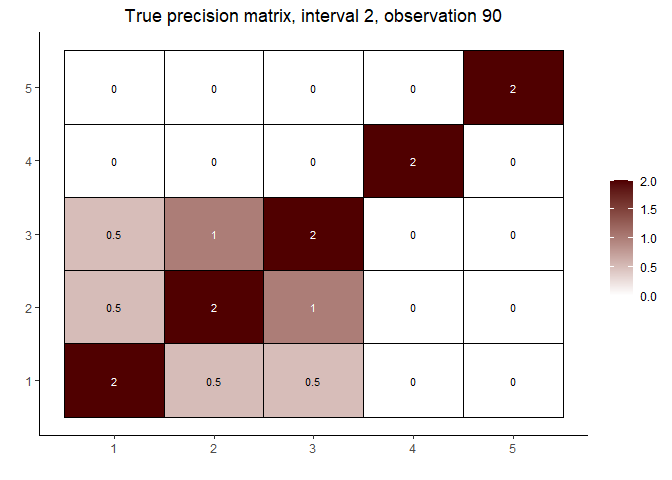
#>
#> [[3]]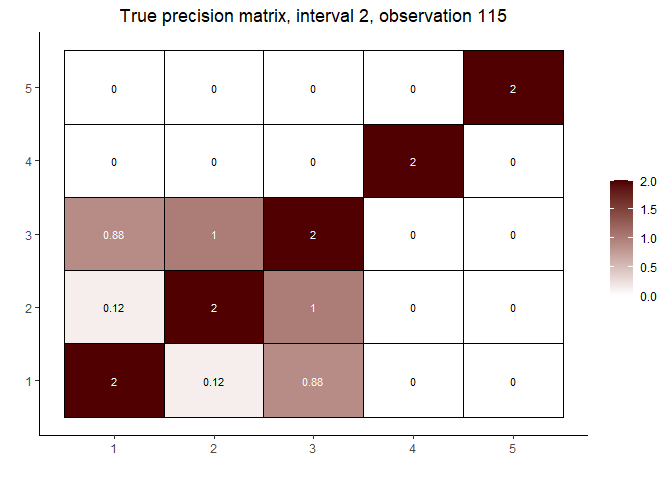
# interval 3
matViz(prec[[length(prec)]], incl_val = TRUE) +
ggtitle(paste0("True precision matrix, interval 3, observations ",
n1 + n2 + 1, ",...,", n1 + n2 + n3))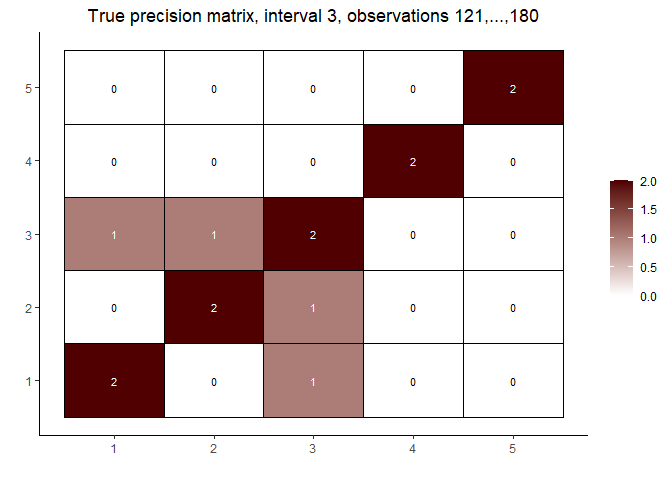
# fit the model and visualize the estimated graphs
(out <- covdepGE(X, Z, parallel = T, num_workers = p))
#> Warning in covdepGE(X, Z, parallel = T, num_workers = p): No registered workers
#> detected; registering doParallel with 5 workers
#> Covariate Dependent Graphical Model
#>
#> ELBO: -171501.68 # Unique Graphs: 3
#> n: 180, variables: 5 Hyperparameter grid size: 125 points
#> Model fit completed in 2.229 secs
plot(out)
#> [[1]]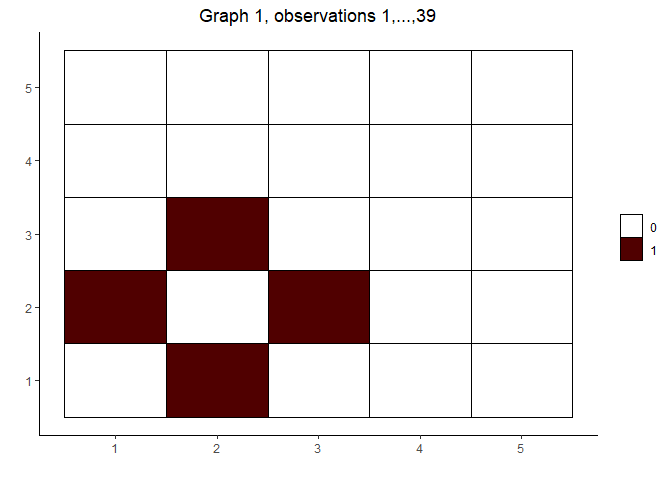
#>
#> [[2]]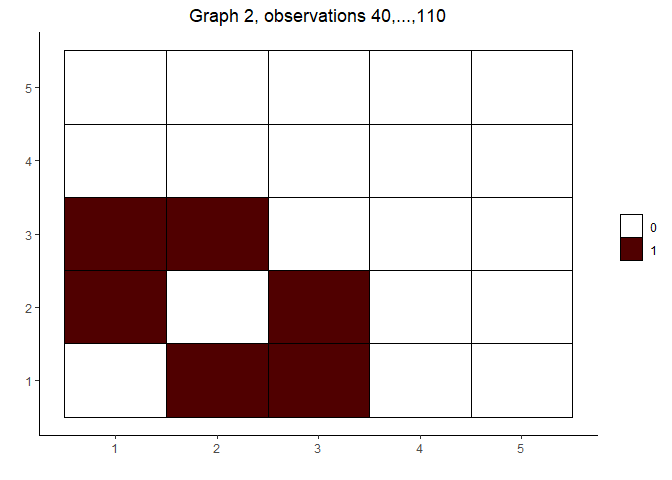
#>
#> [[3]]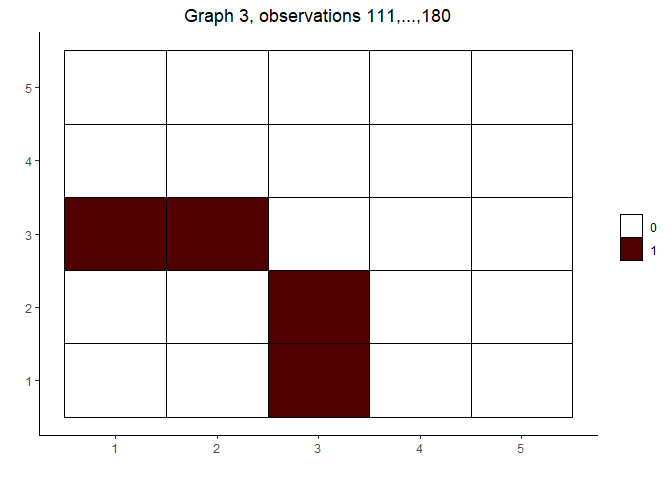
# visualize the posterior inclusion probabilities for variables (1, 3) and (1, 2)
inclusionCurve(out, 1, 2)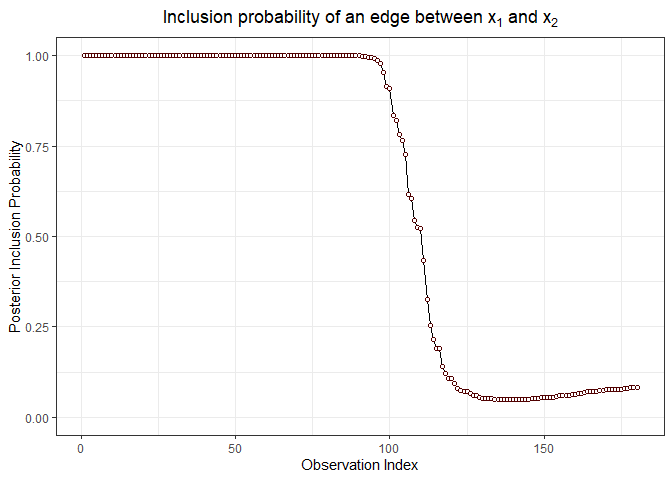
inclusionCurve(out, 1, 3)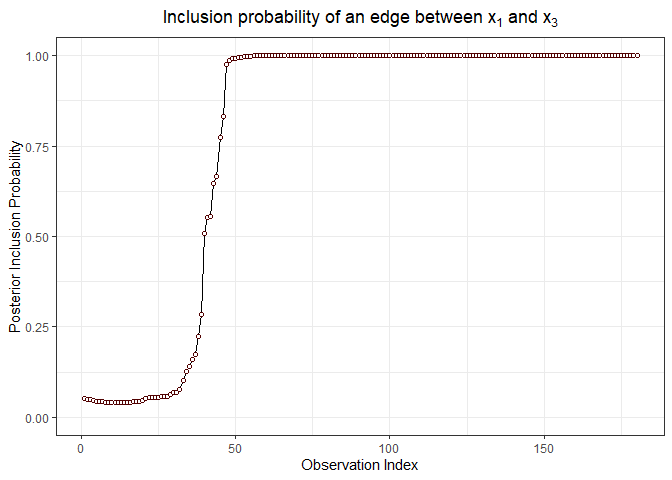
Math is correctly rendered in the version of this document available on CRAN.
Suppose that \(X\) is a \(p\)-dimensional data matrix with \(n\) observations and that \(Z\) is a \(q\)-dimensional extraneous covariate, also with \(n\) observations, where the \(l\)-th observation in \(Z\) is associated with the \(l\)-th observation in \(X\). Further suppose that the \(l\)-th row of \(X\) follows a \(p\)-dimensional Gaussian distribution with mean \(0\) and precision matrix \(\Omega(z_l)\), where \(z_l\) is the \(l\)-th entry of \(Z\) and \(\Omega\) is a continuous function mapping from the space of extraneous covariates to the space of \(p \times p\) non-singular matrices. Then, for the \(l\)-th observation, the \((j,k)\) entry of \(\Omega(z_l)\) is non-zero if, and only if, variable \(j\) and variable \(k\) are dependent given the remaining variables in \(X\).
Given data satisfying these assumptions, the covdepGE
function employs the algorithm described in (1) to estimate a graphical
representation of the structure of \(\Omega\) for each of the observations in
\(X\) as a continuous function of \(Z\). This graph contains an undirected edge
between two variables \(X_j\) and \(X_k\) if, and only if, \(X_j\) and \(X_k\) are conditionally dependent given the
remaining variables. Core components of this methodology are the
weighted pseudo-likelihood framework in which inference is conducted via
a block mean-field variational approximation.
Graphs are constructed using a pseudo-likelihood approach by fixing
each of the columns \(X_j\) of \(X\) as the response and performing a
spike-and-slab regression using the remaining variables \(X_k\) in \(X\) as predictors. To determine if an edge
should be added between \(X_j\) and
\(X_k\), the posterior inclusion
probability of \(X_k\) in a regression
with \(X_j\) fixed as the response
(\(PIP_j(X_k)\)) and vice versa (\(PIP_k(X_j)\)) are symmetrized according to
sym_method (e.g., by taking the mean of \(PIP_k(X_j)\) and \(PIP_j(X_k)\)). If the symmetrized \(PIP\) is greater than
edge_threshold, an edge will be included between \(X_j\) and \(X_k\).
To model \(\Omega\) as a function of \(Z\), \(n\) weighted spike-and-slab regressions are performed for each variable \(X_j\) fixed as the response. The similarity weights for the \(l\)-th regression are taken with respect to observation \(l\) such that observations having similar values of \(Z\) will have larger weights. These similarity weights in conjunction with the pseudo-likelihood framework comprise the weighted pseudo-likelihood approach introduced by (1). Note that model performance is best when \(n > p\).
Spike-and-slab posterior quantities are estimated using a block mean-field variational approximation. Coordinate Ascent Variational Inference (CAVI) is performed for each of the weighted regressions to select the variational parameters that maximize the ELBO. The parameters for each of the regression coefficients are the mean and variance of the slab (\(\mu\) and \(\sigma^2_{\text{var}}\), respectively) and the probability that the coefficient is non-zero (\(\alpha\)). \(\mu\) and \(\alpha\) for all coefficients are initialized as \(0\) and \(0.2\), respectively.
CAVI for the \(n\) regressions is
performed simultaneously for variable \(X_j\) fixed as the response. With each of
the \(n\) sets of \(\alpha\) as the rows of an \(n \times (p - 1)\) matrix, the CAVI for
variable \(X_j\) is ended for all \(n\) regressions when the Frobenius norm of
the change in the \(\alpha\) matrix is
less than alpha_tol or after max_iter
iterations of CAVI have been performed.
Note that since the regressions performed for variable \(X_j\) and \(X_k\) fixed as the response are independent
of each other, they may be performed in parallel by setting
parallel = T. Registering parallel backend with greater
than \(p\) workers offers no benefit,
since each worker takes on one variable to fix as the response and
perform the \(n\) regressions.
Each regression requires the specification of \(3\) hyperparameters: \(\pi\) (the prior probability of inclusion),
\(\sigma^2\) (the prior residual
variance), and \(\sigma_\beta^2\) (the
prior variance of the slab). covdepGE offers \(3\) methods for hyperparameter
specification via the hp_method argument:
grid_search, model_average, and
hybrid. Empirically, grid_search offers the
best sensitivity and model_average offers the best
specificity, while hybrid sits between the other two
methods in both metrics.
The hyperparameter candidate grid is generated by taking the
Cartesian product between ssq, sbsq, and
pip (candidate values for \(\sigma^2\), \(\sigma_\beta^2\), and \(\pi\), respectively). Each of the methods
gives an approach for selecting points from this grid.
In grid_search, the point from the grid that produces
the model that has the greatest total ELBO is selected, where the total
ELBO is calculated by summing the ELBO for each of the \(n\) regressions for a variable \(X_j\) fixed as the response. Thus, all
observations use the same set of hyperparameters for the regression on
\(X_j\).
Instead of selecting only one model as in grid_search,
models are averaged over in model_average. With \(X_j\) fixed as the response, the
unnormalized weights for each grid point used to perform this averaging
is calculated by exponentiating the ELBO for each of the \(n\) regressions. Note that since the ELBO
for a given grid point will vary across the \(n\) regressions due to differing similarity
weights, each of the \(n\) sets of
averaging weights will be unique.
Finally, hybrid combines grid_search and
model_average. Fixing \(X_j\) as the response, for each \(\pi\) candidate in pip, the
point in the grid defined by the Cartesian product of ssq
and sbsq is selected by maximizing the total ELBO summed
across the \(n\) regressions. The
resulting models for each of the \(\pi\) candidates are then averaged using
the exponentiated ELBO for each of the \(n\) regressions as the unnormalized
averaging weights.
Note that in the search step of grid_search and
hybrid, CAVI for each of the grid points is performed for
at most max_iter_grid iterations. A second CAVI is then
performed for max_iter iterations using the \(n\) models that maximized the total ELBO in
the first step. Setting max_iter_grid to be less than
max_iter (as is the default) will result in a more
efficient search.
The candidate grids (ssq, sbsq, and
pip) may be passed as arguments, however, by default, these
grids are generated automatically. Each of the grids are spaced
uniformly between an upper end point and lower end point. The number of
points in each grid is \(5\) by
default. Grids include end points, and the number of points in each grid
is controlled by the arguments nssq, nsbsq,
and npip. The lower endpoints (ssq_lower,
sbsq_lower, and pip_lower) are all
1e-5 by default. The upper endpoints are calculated
dependent on the variable \(X_j\) fixed
as the response.
ssq_upper is simply the variance of \(X_j\) times ssq_mult. By
default, ssq_mult is 1.5.
pip_upper is calculated by regressing the remaining
variables on \(X_j\) using LASSO. The
shrinkage hyperparameter for LASSO is chosen to be
lambda.1se. The number of non-zero coefficients estimated
by LASSO is then divided by p - 1 to calculate
pip_upper. Note that if the LASSO estimate to the number of
non-zero coefficients is \(0\) or \(p - 1\), this estimate is changed to \(1\) or \(p -
2\) (respectively) to ensure that pip_upper is
greater than \(0\) and less than \(1\).
Finally, an upper bound is induced on \(\sigma_\beta^2\) by deriving a rough upper
bound for the signal-to-noise ratio that depends on \(\sigma_\beta^2\). Let \(S^2\) be the sum of the sample variances of
the columns of the predictors \(X’\).
Under the simplifying assumptions that the expected values of \(X’\) and the spike-and-slab regression
coefficients \(\beta\) are \(0\) and that \(X’\) and \(\beta\) are independent, the variance of
the dot product of \(X’\) with \(\beta\) is \(\pi\cdot \sigma^2 \cdot\sigma_\beta^2\cdot
S^2\). Thus, the signal-to-noise ratio under these assumptions is
given by \(\pi\cdot \sigma_\beta^2\cdot
S^2\). Replacing \(\pi\) with
pip_upper and \(\sigma_\beta^2\) with
sbsq_upper gives an upper bound on the signal-to-noise
ratio. Setting this bound equal to snr_upper gives an
expression for sbsq_upper.
The similarity weight for observation \(k\) with respect to observation \(l\) is \(\phi_{\tau_l}(||z_l - z_k||)\). Here, \(|| \cdot ||\) denotes the norm specified by
the norm argument, \(z_l\)
and \(z_k\) are the values of \(Z\) for the \(l\)-th and \(k\)-th observations, \(\phi_{\tau_l}\) is the univariate Gaussian
density with standard deviation \(\tau_l\), and \(\tau_l\) is the bandwidth for the \(l\)-th observation.
tau may be passed as an argument, however, by default,
it is estimated using the methodology given in (2). (2) describes a
two-step approach for density estimation, where in the first step, an
initial estimate is calculated using Silverman’s rule of thumb for
initializing bandwidth values, and in the second step, the density is
refined by updating the bandwidth values. This methodology is used here
to estimate the density of \(Z\), and
the updated bandwidths from the second step are used for
tau.
Sutanoy Dasgupta, Peng Zhao, Prasenjit Ghosh, Debdeep Pati, and Bani Mallick. An approximate Bayesian approach to covariate-dependent graphical modeling. pages 1–59, 2022.
Sutanoy Dasgupta, Debdeep Pati, and Anuj Srivastava. A Two-Step Geometric Framework For Density Modeling. Statistica Sinica, 30(4):2155–2177, 2020.